マルコフの不等式 (Markov's inequality)
正の値を取る確率変数\(X\)について
\[ \mathbb{P}[X\ge t]\le\frac{\mathbb{E}[X]}{t}\]
が成立する。これをMarkovの不等式という。これを示す。
まず\(t\mathbb{I}[X\ge t]\le X\)を確認する。ここで\(\mathbb{I}\)は指示関数とする(本当は1のmathbbmを出したいんやがMathjaxでやってもでないんよな)。これは横軸\(t\)のグラフを書いてみれば明らかです。
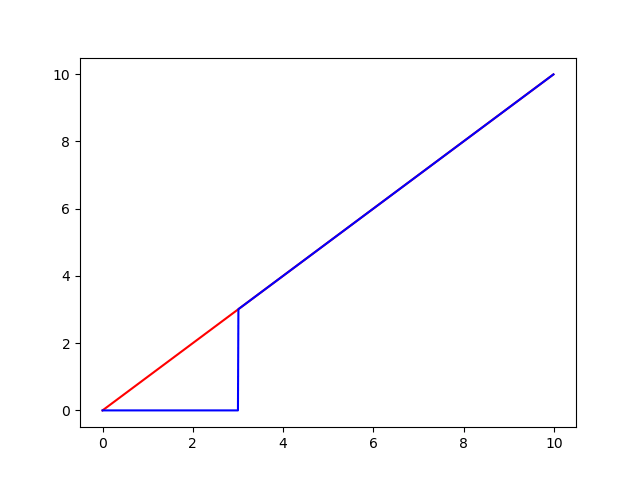
横軸が\(X\)で縦軸が\(Y\)でいずれも確率変数です。青い線が左辺で\(Y=t\mathbb{I}[X\ge t]\)、赤線は右辺でそのまま\(Y=X\)です。図は\(t=3\)の場合ですがどのような\(t\)でも成り立つことは明らかでしょう。赤は常に青以上です。ここで両辺の期待値を取ります。
\[ \begin{align} t\mathbb{I}[X\ge t]&\le X\\ \mathbb{E}[t\mathbb{I}[X\ge t]]&\le \mathbb{E}[X]\\ t\mathbb{P}[X\ge t]&\le\mathbb{E}[X]\\ \mathbb{P}[X\ge t]&\le\frac{\mathbb{E}[X]}t \end{align}\]
ここで1個だけ「うん?」ってなるのが2行目から3行目の左辺ですね。これは定義に従って計算すればよいです。\(\mathbb{E}\)の中身は、\(X\)が\(t\)より大きければ\(t\)、そうでなければ\(0\)となるような確率変数です。これを踏まえると
\[ \begin{align} \mathbb{E}[t\mathbb{I}[X\ge t]]&=t\times\mathbb{P}[X\ge t]+0\times\mathbb{P}[X\lt t]\\&=t\mathbb{P}[X\ge t] \end{align}\]
です。単純な場合分けです。具体的な積分とか総和とか確率変数が連続だとか考えなくても通用しますね。以上で完全にMarkovの不等式が示せました。極めて初等的な操作だけしかやっていませんね。
チェビシェフの不等式(Chebyshev's inequality)
同じように、\(X\)を確率変数とします。\(\mu=\mathbb{E}[X]\)を確率変数の平均値とすると次が成り立つ。
\[ \mathbb{P}[|X-\mu|\ge t]\le\frac{\mathrm{var}[X]}{t^2}\]
\(\mathrm{var}[X]\)は確率変数\(X\)の分散で\(\mathbb{E}[(X-\mu)^2]\)と同じ。これをChebyshevの不等式という。これを示す。
やることは全く同じです。まずは\(t^2\mathbb{I}[|X-\mu|\ge t]\le (X-\mu)^2\)を確認しましょう。先ほどと同じように図を書いてみます。すると次のようになります。
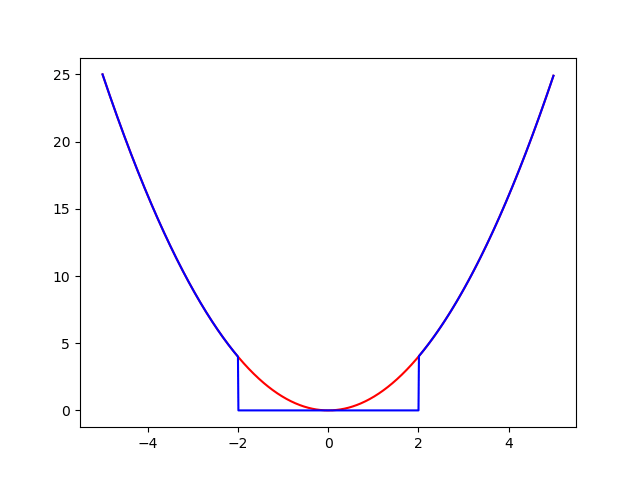
同じですね。青が左辺で赤が右辺を\(Y\)とおいたもの。この図では\(\mu=0\)で、\(t=2\)ですね。常に赤は青以上です。これで示せたも当然です。念のために些細な式変形を書き下しておくと次です。
\[ \begin{align} t^2\mathbb{I}[|X-\mu|\ge t]&\le(X-\mu)^2\\ \mathbb{E}[t^2\mathbb{I}[|X-\mu|\ge t]&\le\mathbb{E}[(X-\mu)^2]\\ t^2\mathbb{P}[|X-\mu|\ge t]&\le\mathrm{var}[X]\\ \mathbb{P}[|X-\mu|\ge t]&\le\frac{\mathrm{var}[X]}{t^2} \end{align}\]
以上でChebyshevの不等式が示せました。両者は名前は違うけどほとんど同じものだということがわかりました。これなら他の不等式をもとにして確率と期待値に関する不等式が作れそうと思うでしょう。実際できます。
チェビシェフの一般化
チェビシェフの不等式で「2乗」としていたところを\(k\)乗にしても成立することは容易に確かめられます。当然ながら2乗のときにはなかった右辺の絶対値記号は必要です。
\[ \mathbb{P}[|X-\mu|\ge t]\le\frac{\mathbb{E}[|X-\mu|^k]}{t^k}\]
がさっきと同じ設定で成立する。ただし\(k\ge 0\)。\(k\)ゼロはまあ意味ないけど間違ってないので入れておく。
右辺は確率変数\(X\)の平均周りの\(k\)次モーメントです。一般的に存在するわけではありませんが存在するならこの手の不等式が成立するってことです。次に思いつくのはもっと他の、多項式以外の\(|X-\mu|\)に関する関数を考えることです。多項式以外の初等関数というと指数関数とかです。そうです。指数関数について考えます。
Chernoff型の不等式
\(\mathbb{E}[e^{\lambda(X-\mu)}]\)という値がある\(\lambda\in[0,b]\)で存在するとする。このとき次式が成立。
\[ \mathbb{P}[(X-\mu)\ge t] \le\inf_{\lambda\in[0,b]}\frac{\mathbb{E}[e^{\lambda (X-\mu)}]}{e^{\lambda t}}\]
\(\mathbb{E}[e^{\lambda(X-\mu)}]\)はモーメント母関数といわれています。この形式の不等式をChernoff型の不等式といいます。実際には、\(X\)に関するいろいろな仮定で右辺はより具体的になるのでここでは「型の」といっておきます。これを示すことは簡単です。これまでの議論を関数\(Y=e^{\lambda(X-\mu)}\)に対して適用すればよいです。同じようにして\(\mathbb{P}\)の内側だけ0に落ちるような関数との比較からスタートすればいい。
右辺を具体的に計算するにあたって、両辺の対数を取った次の形式が用いられることがあります。
\[ \log\mathbb{P}[(X-\mu)\ge t] \le\inf_{\lambda\in[0,b]}\{\log\mathbb{E}[e^{\lambda(X-\mu)}]-\lambda t\}\]
チェビシェフ一般化とChernoffの関係
前述のChebyshevの不等式を一般化した多項式モーメントの式と、Chernoff型の不等式は左辺が同じものです。おっと、Chebyshevの方には絶対値がついているのでここでは\(X-\mu>0\)とでもしておく。Markovの不等式では実は\(X\ge 0\)としていたのでそれと同じようなもん。
話を戻すと、左辺が同じ不等式ならどっちかが有効でどっちかが冗長なはずです。つまりどっちが等号成立により近いか、あるいはtightであるかsharpであるかなどといったりします。なのでここではChernoff型とChebyshevの不等式を一般化した多項式モーメントの不等式の、どちらが有効なのかを見てみましょう。結論からいうと\(k\)を最適に選べばChernoff型が多項式モーメントよりもtightになることはありません。
でもChernoffの方が右辺が計算しやすいとか何とかで応用所よく使われるそうです。
つづき
\(X\sim\mathcal{N}(\mu,\sigma^2)\)としたとき、つまり\(X\)が正規分布に従うとした場合Chernoff型の不等式の右辺は具体的にどうなるか?
余談
ここまで読んでなんでChebyshevとかチェビシェフとか統一しやんねんと思った人挙手。
参考文献
Martin J. Wainwright, High-Dimensional Statistics, A Non-Asymptotic Viewpoint, 2019, Cambridge University Press, pp. 21-22, https://doi.org/10.1017/9781108627771.