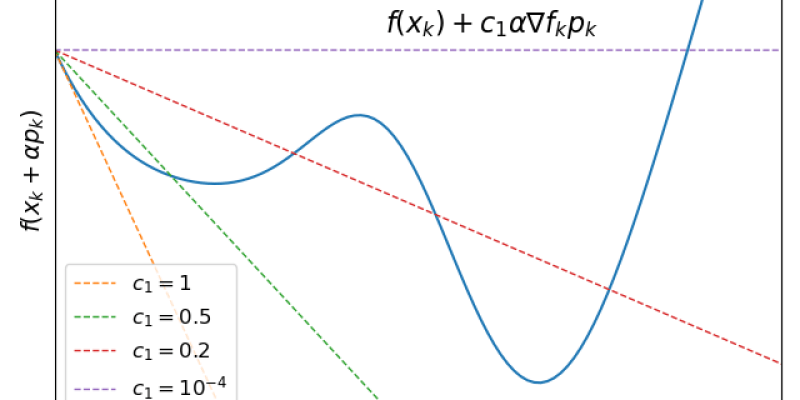
非厳密直線探索の終了条件。
BFGS公式による準ニュートン(Quasi-Newton)法はいまのところ実用上最も優れているといえる最適化手法だ。超1次収束かつ各反復における計算オーダが変数の数の2乗で済むため、変数の2乗が許容される規模の問題である限り実用的にベストな解法として使われる。
Reference Chapter4. of Non-convex Optimization for Machine Learning https://arxiv.org/abs/1712.07897 "Alternating Minimization".
前ページ、一般的な交互最小化の収束性についての続きです。
補題1 Bistable Pointの必要十分条件
関数\(f:\mathbb{R}^p\times\mathbb{R}^q\to\mathbb{R}\)が連続微分可能で、それぞれの変数について周辺凸関数であるとき、点\((x,y)\)がbistableであることと\(\nabla f(x,y)=0\)であることは同値。
Reference Chapter4. of Non-convex Optimization for Machine Learning https://arxiv.org/abs/1712.07897 "Alternating Minimization".
多変数関数における変数の分割
関数\(f:\mathbb{R}^d\to\mathbb{R}\)を目的関数とする最小化問題について考える。\(d=p+q\)なる\(p,q\)を用いて関数\(f\)を\(f:\mathbb{R}^p\times\mathbb{R}^q\to\mathbb{R}\)と見なすことが出来る。これは変数の内\(p\)個のサブセットを取ってきて変数を分割しただけ。残った変数\(q\)個をまた別な変数とおく。これを\((x,y)\in\mathbb{R}^p\times\mathbb{R}^q\)として新たに\(f(x,y)\)とおく。よりたくさんの変数に分割する場合にも2分割を繰り返せばよいので一般性を失っていない。制約集合による条件\((x,y)\in\mathcal{X}\times\mathcal{Y}\)を考えてもよい。一般にはそれぞれの制約集合が独立にな条件で与えられているとは限らないので\((x,y)\in\mathcal{Z}\subset\mathbb{R}^p\times\mathbb{R}^q\)という形になることに注意せよ。
Pythonで3層ニューラルネットの勾配を計算
3層ニューラルネットとは、入力層・中間層・出力層の3層によって構成される多層パーセプトロンで、回帰モデルの1つといえる。ここではその勾配の計算方法とその行列表示をまとめる。行列表示をすることによってPythonのnumpyだけをつかった勾配計算を簡単に書くことができる。いまは3層のみ、忘れない内にメモる。