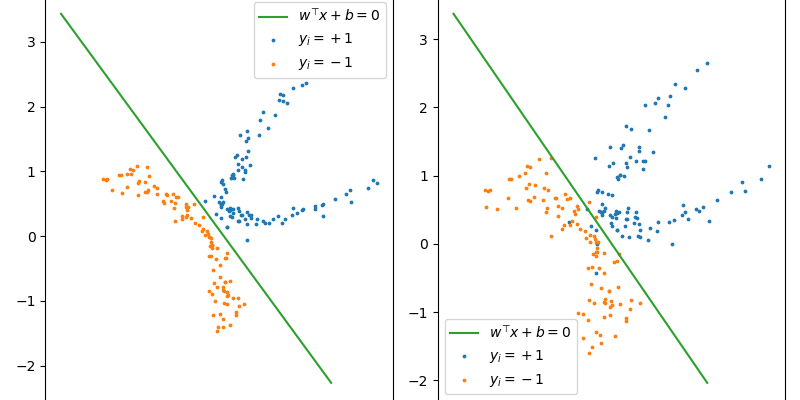BFGS公式による準ニュートン（Quasi-Newton）法はいまのところ実用上最も優れているといえる最適化手法だ。超1次収束かつ各反復における計算オーダが変数の数の2乗で済むため、変数の2乗が許容される規模の問題である限り実用的にベストな解法として使われる。

サポートベクターマシンの導出からPythonによる2次計画ソルバの利用まで。 サポートベクターマシンとPythonによる2次計画問題：基底展開とカーネル関数の導入に続いている。

Rieszの表現定理は、ヒルベルト空間上の任意の有界線形汎関数がそのヒルベルト空間のある元との内積によって表現できて、その方法は一意であることを言っている。これをメモっておく。

汎関数の勾配（functional gradient）をベクトル微分の一般化として納得する。

グラフラプラシアン（Graph Laplacian）がなぜラプラシアンと呼ばれるのかを、普通の関数に対するラプラシアンオペレータと比較して直観的に説明する。ついでに普通の関数のときにラプラシアンとまとめて紹介されるナブラについて、それに対応する接続行列について紹介する。